Chapter 7: Probability
Learning Outcomes
- Compute a conditional probability for an event
- Use Baye’s theorem to compute a conditional probability
- Calculate the expected value of an event
In the next section, we will explore more complex conditional probabilities and ways to compute them. Conditional probabilities can give us information such as the likelihood of getting a positive test result for a disease without actually having the disease. If a doctor thinks the chances that a positive test result nearly guarantees that a patient has a disease, they might begin an unnecessary and possibly harmful treatment regimen on a healthy patient. If you were to get a positive test result, knowing the likelihood of getting a false positive can guide you to get a second opinion.
Bayes’ Theorem
In this section we concentrate on the more complex conditional probability problems we began looking at in the last section.
For example, suppose a certain disease has an incidence rate of 0.1% (that is, it afflicts 0.1% of the population). A test has been devised to detect this disease. The test does not produce false negatives (that is, anyone who has the disease will test positive for it), but the false positive rate is 5% (that is, about 5% of people who take the test will test positive, even though they do not have the disease). Suppose a randomly selected person takes the test and tests positive. What is the probability that this person actually has the disease?
There are two ways to approach the solution to this problem. One involves an important result in probability theory called Bayes’ theorem. We will discuss this theorem a bit later, but for now we will use an alternative and, we hope, much more intuitive approach.
Let’s break down the information in the problem piece by piece as an example.
example
Suppose a certain disease has an incidence rate of 0.1% (that is, it afflicts 0.1% of the population). The percentage 0.1% can be converted to a decimal number by moving the decimal place two places to the left, to get 0.001. In turn, 0.001 can be rewritten as a fraction: 1/1000. This tells us that about 1 in every 1000 people has the disease. (If we wanted we could write P(disease)=0.001.)
A test has been devised to detect this disease. The test does not produce false negatives (that is, anyone who has the disease will test positive for it). This part is fairly straightforward: everyone who has the disease will test positive, or alternatively everyone who tests negative does not have the disease. (We could also say P(positive | disease)=1.)
The false positive rate is 5% (that is, about 5% of people who take the test will test positive, even though they do not have the disease). This is even more straightforward. Another way of looking at it is that of every 100 people who are tested and do not have the disease, 5 will test positive even though they do not have the disease. (We could also say that P(positive | no disease)=0.05.)
Suppose a randomly selected person takes the test and tests positive. What is the probability that this person actually has the disease? Here we want to compute P(disease|positive). We already know that P(positive|disease)=1, but remember that conditional probabilities are not equal if the conditions are switched.
Rather than thinking in terms of all these probabilities we have developed, let’s create a hypothetical situation and apply the facts as set out above. First, suppose we randomly select 1000 people and administer the test. How many do we expect to have the disease? Since about 1/1000 of all people are afflicted with the disease, 1/1000 of 1000 people is 1. (Now you know why we chose 1000.) Only 1 of 1000 test subjects actually has the disease; the other 999 do not.
We also know that 5% of all people who do not have the disease will test positive. There are 999 disease-free people, so we would expect (0.05)(999)=49.95 (so, about 50) people to test positive who do not have the disease.
Now back to the original question, computing P(disease|positive). There are 51 people who test positive in our example (the one unfortunate person who actually has the disease, plus the 50 people who tested positive but don’t). Only one of these people has the disease, so
P(disease | positive) [latex]\approx\frac{1}{51}\approx0.0196[/latex]
or less than 2%. Does this surprise you? This means that of all people who test positive, over 98% do not have the disease.
The answer we got was slightly approximate, since we rounded 49.95 to 50. We could redo the problem with 100,000 test subjects, 100 of whom would have the disease and (0.05)(99,900)=4995 test positive but do not have the disease, so the exact probability of having the disease if you test positive is
P(disease | positive) [latex]\approx\frac{100}{5095}\approx0.0196[/latex]
which is pretty much the same answer.
But back to the surprising result. Of all people who test positive, over 98% do not have the disease. If your guess for the probability a person who tests positive has the disease was wildly different from the right answer (2%), don’t feel bad. The exact same problem was posed to doctors and medical students at the Harvard Medical School 25 years ago and the results revealed in a 1978 New England Journal of Medicine article. Only about 18% of the participants got the right answer. Most of the rest thought the answer was closer to 95% (perhaps they were misled by the false positive rate of 5%).
So at least you should feel a little better that a bunch of doctors didn’t get the right answer either (assuming you thought the answer was much higher). But the significance of this finding and similar results from other studies in the intervening years lies not in making math students feel better but in the possibly catastrophic consequences it might have for patient care. If a doctor thinks the chances that a positive test result nearly guarantees that a patient has a disease, they might begin an unnecessary and possibly harmful treatment regimen on a healthy patient. Or worse, as in the early days of the AIDS crisis when being HIV-positive was often equated with a death sentence, the patient might take a drastic action and commit suicide.
This example is worked through in detail in the video here.
As we have seen in this hypothetical example, the most responsible course of action for treating a patient who tests positive would be to counsel the patient that they most likely do not have the disease and to order further, more reliable, tests to verify the diagnosis.
One of the reasons that the doctors and medical students in the study did so poorly is that such problems, when presented in the types of statistics courses that medical students often take, are solved by use of Bayes’ theorem, which is stated as follows:
Bayes’ Theorem
[latex]P(A|B)=\frac{P(A)P(B|A)}{P(A)P(B|A)+P(\bar{A})P(B|\bar{A})}[/latex]
In our earlier example, this translates to
[latex]P(\text{disease}|\text{positive})=\frac{P(\text{disease})P(\text{positive}|\text{disease})}{P(\text{disease})P(\text{positive}|\text{disease})+P(\text{nodisease})P(\text{positive}|\text{nodisease})}[/latex]
Plugging in the numbers gives
[latex]P(\text{disease}|\text{positive})=\frac{(0.001)(1)}{(0.001)(1)+(0.999)(0.05)}\approx0.0196[/latex]
which is exactly the same answer as our original solution.
The problem is that you (or the typical medical student, or even the typical math professor) are much more likely to be able to remember the original solution than to remember Bayes’ theorem. Psychologists, such as Gerd Gigerenzer, author of Calculated Risks: How to Know When Numbers Deceive You, have advocated that the method involved in the original solution (which Gigerenzer calls the method of “natural frequencies”) be employed in place of Bayes’ Theorem. Gigerenzer performed a study and found that those educated in the natural frequency method were able to recall it far longer than those who were taught Bayes’ theorem. When one considers the possible life-and-death consequences associated with such calculations it seems wise to heed his advice.
example
A certain disease has an incidence rate of 2%. If the false negative rate is 10% and the false positive rate is 1%, compute the probability that a person who tests positive actually has the disease.
Solution:
Imagine 10,000 people who are tested. Of these 10,000, 200 will have the disease; 10% of them, or 20, will test negative and the remaining 180 will test positive. Of the 9800 who do not have the disease, 98 will test positive. So of the 278 total people who test positive, 180 will have the disease. Thus
[latex]P(\text{disease}|\text{positive})=\frac{180}{278}\approx0.647[/latex]
so about 65% of the people who test positive will have the disease.
Using Bayes theorem directly would give the same result:
[latex]P(\text{disease}|\text{positive})=\frac{(0.02)(0.90)}{(0.02)(0.90)+(0.98)(0.01)}=\frac{0.018}{0.0278}\approx0.647[/latex]
View the following for more about this example.
Counting
Counting? You already know how to count or you wouldn’t be taking a college-level math class, right? Well yes, but what we’ll really be investigating here are ways of counting efficiently. When we get to the probability situations a bit later in this chapter we will need to count some very large numbers, like the number of possible winning lottery tickets. One way to do this would be to write down every possible set of numbers that might show up on a lottery ticket, but believe me: you don’t want to do this.
Basic Counting
We will start, however, with some more reasonable sorts of counting problems in order to develop the ideas that we will soon need.
example
Suppose at a particular restaurant you have three choices for an appetizer (soup, salad or breadsticks) and five choices for a main course (hamburger, sandwich, quiche, fajita or pizza). If you are allowed to choose exactly one item from each category for your meal, how many different meal options do you have?
Solution 1: One way to solve this problem would be to systematically list each possible meal:
soup + hamburger soup + sandwich soup + quiche
soup + fajita soup + pizza salad + hamburger
salad + sandwich salad + quiche salad + fajita
salad + pizza breadsticks + hamburger breadsticks + sandwich
breadsticks + quiche breadsticks + fajita breadsticks + pizza
Assuming that we did this systematically and that we neither missed any possibilities nor listed any possibility more than once, the answer would be 15. Thus you could go to the restaurant 15 nights in a row and have a different meal each night.
Solution 2: Another way to solve this problem would be to list all the possibilities in a table:
| hamburger | sandwich | quiche | fajita | pizza | |
| soup | soup+burger | ||||
| salad | salad+burger | ||||
| bread | etc |
In each of the cells in the table we could list the corresponding meal: soup + hamburger in the upper left corner, salad + hamburger below it, etc. But if we didn’t really care what the possible meals are, only how many possible meals there are, we could just count the number of cells and arrive at an answer of 15, which matches our answer from the first solution. (It’s always good when you solve a problem two different ways and get the same answer!)
Solution 3: We already have two perfectly good solutions. Why do we need a third? The first method was not very systematic, and we might easily have made an omission. The second method was better, but suppose that in addition to the appetizer and the main course we further complicated the problem by adding desserts to the menu: we’ve used the rows of the table for the appetizers and the columns for the main courses—where will the desserts go? We would need a third dimension, and since drawing 3-D tables on a 2-D page or computer screen isn’t terribly easy, we need a better way in case we have three categories to choose form instead of just two.
So, back to the problem in the example. What else can we do? Let’s draw a tree diagram:
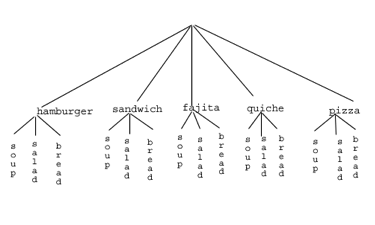
This is called a “tree” diagram because at each stage we branch out, like the branches on a tree. In this case, we first drew five branches (one for each main course) and then for each of those branches we drew three more branches (one for each appetizer). We count the number of branches at the final level and get (surprise, surprise!) 15.
If we wanted, we could instead draw three branches at the first stage for the three appetizers and then five branches (one for each main course) branching out of each of those three branches.
OK, so now we know how to count possibilities using tables and tree diagrams. These methods will continue to be useful in certain cases, but imagine a game where you have two decks of cards (with 52 cards in each deck) and you select one card from each deck. Would you really want to draw a table or tree diagram to determine the number of outcomes of this game?
Let’s go back to the previous example that involved selecting a meal from three appetizers and five main courses, and look at the second solution that used a table. Notice that one way to count the number of possible meals is simply to number each of the appropriate cells in the table, as we have done above. But another way to count the number of cells in the table would be multiply the number of rows (3) by the number of columns (5) to get 15. Notice that we could have arrived at the same result without making a table at all by simply multiplying the number of choices for the appetizer (3) by the number of choices for the main course (5). We generalize this technique as the basic counting rule:
Basic Counting Rule
If we are asked to choose one item from each of two separate categories where there are m items in the first category and n items in the second category, then the total number of available choices is m · n.
This is sometimes called the multiplication rule for probabilities.
example
There are 21 novels and 18 volumes of poetry on a reading list for a college English course. How many different ways can a student select one novel and one volume of poetry to read during the quarter?
Solution:
There are 21 choices from the first category and 18 for the second, so there are 21 · 18 = 378 possibilities.
The Basic Counting Rule can be extended when there are more than two categories by applying it repeatedly, as we see in the next example.
example
Suppose at a particular restaurant you have three choices for an appetizer (soup, salad or breadsticks), five choices for a main course (hamburger, sandwich, quiche, fajita or pasta) and two choices for dessert (pie or ice cream). If you are allowed to choose exactly one item from each category for your meal, how many different meal options do you have?
Solution:
There are 3 choices for an appetizer, 5 for the main course and 2 for dessert, so there are 3 · 5 · 2 = 30 possibilities.
Example
A quiz consists of 3 true-or-false questions. In how many ways can a student answer the quiz?
Solution:
There are 3 questions. Each question has 2 possible answers (true or false), so the quiz may be answered in 2 · 2 · 2 = 8 different ways. Recall that another way to write 2 · 2 · 2 is 23, which is much more compact.
Basic counting examples from this section are described in the following video.
Click here to view this video.
Permutations
In this section we will develop an even faster way to solve some of the problems we have already learned to solve by other means. Let’s start with a couple examples.
example
How many different ways can the letters of the word MATH be rearranged to form a four-letter code word?
Solution:
This problem is a bit different. Instead of choosing one item from each of several different categories, we are repeatedly choosing items from the same category (the category is: the letters of the word MATH) and each time we choose an item we do not replace it, so there is one fewer choice at the next stage: we have 4 choices for the first letter (say we choose A), then 3 choices for the second (M, T and H; say we choose H), then 2 choices for the next letter (M and T; say we choose M) and only one choice at the last stage (T). Thus there are 4 · 3 · 2 · 1 = 24 ways to spell a code worth with the letters MATH.
In this example, we needed to calculate n · (n – 1) · (n – 2) ··· 3 · 2 · 1. This calculation shows up often in mathematics, and is called the factorial, and is notated n!
Factorial
n! = n · (n – 1) · (n – 2) ··· 3 · 2 · 1
example
How many ways can five different door prizes be distributed among five people?
Solution:
There are 5 choices of prize for the first person, 4 choices for the second, and so on. The number of ways the prizes can be distributed will be 5! = 5 · 4 · 3 · 2 · 1 = 120 ways.
Now we will consider some slightly different examples.
examples
A charity benefit is attended by 25 people and three gift certificates are given away as door prizes: one gift certificate is in the amount of $100, the second is worth $25 and the third is worth $10. Assuming that no person receives more than one prize, how many different ways can the three gift certificates be awarded?
Solution:
Using the Basic Counting Rule, there are 25 choices for the person who receives the $100 certificate, 24 remaining choices for the $25 certificate and 23 choices for the $10 certificate, so there are 25 · 24 · 23 = 13,800 ways in which the prizes can be awarded.
Example
Eight sprinters have made it to the Olympic finals in the 100-meter race. In how many different ways can the gold, silver and bronze medals be awarded?
Solution:
Using the Basic Counting Rule, there are 8 choices for the gold medal winner, 7 remaining choices for the silver, and 6 for the bronze, so there are 8 · 7 · 6 = 336 ways the three medals can be awarded to the 8 runners.
Note that in these preceding examples, the gift certificates and the Olympic medals were awarded without replacement; that is, once we have chosen a winner of the first door prize or the gold medal, they are not eligible for the other prizes. Thus, at each succeeding stage of the solution there is one fewer choice (25, then 24, then 23 in the first example; 8, then 7, then 6 in the second). Contrast this with the situation of a multiple choice test, where there might be five possible answers — A, B, C, D or E — for each question on the test.
Note also that the order of selection was important in each example: for the three door prizes, being chosen first means that you receive substantially more money; in the Olympics example, coming in first means that you get the gold medal instead of the silver or bronze. In each case, if we had chosen the same three people in a different order there might have been a different person who received the $100 prize, or a different goldmedalist. (Contrast this with the situation where we might draw three names out of a hat to each receive a $10 gift certificate; in this case the order of selection is not important since each of the three people receive the same prize. Situations where the order is not important will be discussed in the next section.)
Factorial examples are worked in this video.
We can generalize the situation in the two examples above to any problem without replacement where the order of selection is important. If we are arranging in order r items out of n possibilities (instead of 3 out of 25 or 3 out of 8 as in the previous examples), the number of possible arrangements will be given by
n · (n – 1) · (n – 2) ··· (n – r + 1)
If you don’t see why (n — r + 1) is the right number to use for the last factor, just think back to the first example in this section, where we calculated 25 · 24 · 23 to get 13,800. In this case n = 25 and r = 3, so n — r + 1 = 25 — 3 + 1 = 23, which is exactly the right number for the final factor.
Now, why would we want to use this complicated formula when it’s actually easier to use the Basic Counting Rule, as we did in the first two examples? Well, we won’t actually use this formula all that often; we only developed it so that we could attach a special notation and a special definition to this situation where we are choosing r items out of n possibilities without replacement and where the order of selection is important. In this situation we write:
Permutations
nPr = n · (n – 1) · (n – 2) ··· (n – r + 1)
We say that there are nPr permutations of size r that may be selected from among n choices without replacement when order matters.
It turns out that we can express this result more simply using factorials.
[latex]{}_{n}{{P}_{r}}=\frac{n!}{(n-r)!}[/latex]
In practicality, we usually use technology rather than factorials or repeated multiplication to compute permutations.
example
I have nine paintings and have room to display only four of them at a time on my wall. How many different ways could I do this?
Solution:
Since we are choosing 4 paintings out of 9 without replacement where the order of selection is important there are 9P4 = 9 · 8 · 7 · 6 = 3,024 permutations.[/hidden-answer]
Example
How many ways can a four-person executive committee (president, vice-president, secretary, treasurer) be selected from a 16-member board of directors of a non-profit organization?
Solution:
We want to choose 4 people out of 16 without replacement and where the order of selection is important. So the answer is 16P4 = 16 · 15 · 14 · 13 = 43,680.[/hidden-answer]
View this video to see more about the permutations examples.
Try It
How many 5 character passwords can be made using the letters A through Z
- if repeats are allowed
- if no repeats are allowed
Combinations
In the previous section we considered the situation where we chose r items out of n possibilities without replacement and where the order of selection was important. We now consider a similar situation in which the order of selection is not important.
Example
A charity benefit is attended by 25 people at which three $50 gift certificates are given away as door prizes. Assuming no person receives more than one prize, how many different ways can the gift certificates be awarded?
Solution:
Using the Basic Counting Rule, there are 25 choices for the first person, 24 remaining choices for the second person and 23 for the third, so there are 25 · 24 · 23 = 13,800 ways to choose three people. Suppose for a moment that Abe is chosen first, Bea second and Cindy third; this is one of the 13,800 possible outcomes. Another way to award the prizes would be to choose Abe first, Cindy second and Bea third; this is another of the 13,800 possible outcomes. But either way Abe, Bea and Cindy each get $50, so it doesn’t really matter the order in which we select them. In how many different orders can Abe, Bea and Cindy be selected? It turns out there are 6:
ABC ACB BAC BCA CAB CBA
How can we be sure that we have counted them all? We are really just choosing 3 people out of 3, so there are 3 · 2 · 1 = 6 ways to do this; we didn’t really need to list them all. We can just use permutations!
So, out of the 13,800 ways to select 3 people out of 25, six of them involve Abe, Bea and Cindy. The same argument works for any other group of three people (say Abe, Bea and David or Frank, Gloria and Hildy) so each three-person group is counted six times. Thus the 13,800 figure is six times too big. The number of distinct three-person groups will be 13,800/6 = 2300.
We can generalize the situation in this example above to any problem of choosing a collection of items without replacement where the order of selection is not important. If we are choosing r items out of n possibilities (instead of 3 out of 25 as in the previous examples), the number of possible choices will be given by [latex]\frac{{}_{n}{{P}_{r}}}{{}_{r}{{P}_{r}}}[/latex], and we could use this formula for computation. However this situation arises so frequently that we attach a special notation and a special definition to this situation where we are choosing r items out of n possibilities without replacement where the order of selection is not important.
Combinations
[latex]{}_{n}{{C}_{r}}=\frac{{}_{n}{{P}_{r}}}{{}_{r}{{P}_{r}}}[/latex]
We say that there are nCr combinations of size r that may be selected from among n choices without replacement where order doesn’t matter.
We can also write the combinations formula in terms of factorials:
[latex]{}_{n}{{C}_{r}}=\frac{n!}{(n-r)!r!}[/latex]
Example
A group of four students is to be chosen from a 35-member class to represent the class on the student council. How many ways can this be done?
Solution:
Since we are choosing 4 people out of 35 without replacement where the order of selection is not important there are [latex]{}_{35}{{C}_{4}}=\frac{35\cdot34\cdot33\cdot32}{4\cdot3\cdot2\cdot1}[/latex] = 52,360 combinations.
View the following for more explanation of the combinations examples.
Try It
The United States Senate Appropriations Committee consists of 29 members; the Defense Subcommittee of the Appropriations Committee consists of 19 members. Disregarding party affiliation or any special seats on the Subcommittee, how many different 19-member subcommittees may be chosen from among the 29 Senators on the Appropriations Committee?
In the preceding Try It problem we assumed that the 19 members of the Defense Subcommittee were chosen without regard to party affiliation. In reality this would never happen: if Republicans are in the majority they would never let a majority of Democrats sit on (and thus control) any subcommittee. (The same of course would be true if the Democrats were in control.) So let’s consider the problem again, in a slightly more complicated form:
Example
The United States Senate Appropriations Committee consists of 29 members, 15 Republicans and 14 Democrats. The Defense Subcommittee consists of 19 members, 10 Republicans and 9 Democrats. How many different ways can the members of the Defense Subcommittee be chosen from among the 29 Senators on the Appropriations Committee?
Solution:
In this case we need to choose 10 of the 15 Republicans and 9 of the 14 Democrats. There are 15C10 = 3003 ways to choose the 10 Republicans and 14C9 = 2002 ways to choose the 9 Democrats. But now what? How do we finish the problem?
Suppose we listed all of the possible 10-member Republican groups on 3003 slips of red paper and all of the possible 9-member Democratic groups on 2002 slips of blue paper. How many ways can we choose one red slip and one blue slip? This is a job for the Basic Counting Rule! We are simply making one choice from the first category and one choice from the second category, just like in the restaurant menu problems from earlier.
There must be 3003 · 2002 = 6,012,006 possible ways of selecting the members of the Defense Subcommittee.
This example is worked through below.
Probability Using Permutations and Combinations
We can use permutations and combinations to help us answer more complex probability questions.
examples
A 4 digit PIN number is selected. What is the probability that there are no repeated digits?
Solution:
There are 10 possible values for each digit of the PIN (namely: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9), so there are 10 · 10 · 10 · 10 = 104 = 10000 total possible PIN numbers.
To have no repeated digits, all four digits would have to be different, which is selecting without replacement. We could either compute 10 · 9 · 8 · 7, or notice that this is the same as the permutation 10P4 = 5040.
The probability of no repeated digits is the number of 4 digit PIN numbers with no repeated digits divided by the total number of 4 digit PIN numbers. This probability is [latex]\frac{{}_{10}{{P}_{4}}}{{{10}^{4}}}=\frac{5040}{10000}=0.504[/latex]
Example
In a certain state’s lottery, 48 balls numbered 1 through 48 are placed in a machine and six of them are drawn at random. If the six numbers drawn match the numbers that a player had chosen, the player wins $1,000,000. In this lottery, the order the numbers are drawn in doesn’t matter. Compute the probability that you win the million-dollar prize if you purchase a single lottery ticket.
Solution:
In order to compute the probability, we need to count the total number of ways six numbers can be drawn, and the number of ways the six numbers on the player’s ticket could match the six numbers drawn from the machine. Since there is no stipulation that the numbers be in any particular order, the number of possible outcomes of the lottery drawing is 48C6 = 12,271,512. Of these possible outcomes, only one would match all six numbers on the player’s ticket, so the probability of winning the grand prize is:
[latex]\frac{{}_{6}{{C}_{6}}}{{}_{48}{{C}_{6}}}=\frac{1}{12271512}\approx0.0000000815[/latex]
Example
In the state lottery from the previous example, if five of the six numbers drawn match the numbers that a player has chosen, the player wins a second prize of $1,000. Compute the probability that you win the second prize if you purchase a single lottery ticket.
Solution:
As above, the number of possible outcomes of the lottery drawing is 48C6 = 12,271,512. In order to win the second prize, five of the six numbers on the ticket must match five of the six winning numbers; in other words, we must have chosen five of the six winning numbers and one of the 42 losing numbers. The number of ways to choose 5 out of the 6 winning numbers is given by 6C5 = 6 and the number of ways to choose 1 out of the 42 losing numbers is given by 42C1 = 42. Thus the number of favorable outcomes is then given by the Basic Counting Rule: 6C5 · 42C1 = 6 · 42 = 252. So the probability of winning the second prize is.
[latex]\frac{\left({}_{6}{{C}_{5}}\right)\left({}_{42}{{C}_{1}}\right)}{{}_{48}{{C}_{6}}}=\frac{252}{12271512}\approx0.0000205[/latex]
The previous examples are worked in the following video.
examples
Compute the probability of randomly drawing five cards from a deck and getting exactly one Ace.
Solution:
In many card games (such as poker) the order in which the cards are drawn is not important (since the player may rearrange the cards in his hand any way he chooses); in the problems that follow, we will assume that this is the case unless otherwise stated. Thus we use combinations to compute the possible number of 5-card hands, 52C5. This number will go in the denominator of our probability formula, since it is the number of possible outcomes.
For the numerator, we need the number of ways to draw one Ace and four other cards (none of them Aces) from the deck. Since there are four Aces and we want exactly one of them, there will be 4C1 ways to select one Ace; since there are 48 non-Aces and we want 4 of them, there will be 48C4 ways to select the four non-Aces. Now we use the Basic Counting Rule to calculate that there will be 4C1 · 48C4 ways to choose one ace and four non-Aces.
Putting this all together, we have
[latex]P(\text{oneAce})=\frac{\left({}_{4}{{C}_{1}}\right)\left({}_{48}{{C}_{4}}\right)}{{}_{52}{{C}_{5}}}=\frac{778320}{2598960}\approx0.299[/latex]
Example
Compute the probability of randomly drawing five cards from a deck and getting exactly two Aces.
Solution:
The solution is similar to the previous example, except now we are choosing 2 Aces out of 4 and 3 non-Aces out of 48; the denominator remains the same:
[latex]P(\text{twoAces})=\frac{\left({}_{4}{{C}_{2}}\right)\left({}_{48}{{C}_{3}}\right)}{{}_{52}{{C}_{5}}}=\frac{103776}{2598960}\approx0.0399[/latex]
It is useful to note that these card problems are remarkably similar to the lottery problems discussed earlier.
View the following for further demonstration of these examples.
Birthday Problem
Let’s take a pause to consider a famous problem in probability theory:
Take a guess at the answer to the above problem. Was your guess fairly low, like around 10%? That seems to be the intuitive answer (30/365, perhaps?). Let’s see if we should listen to our intuition. Let’s start with a simpler problem, however.
example
Suppose three people are in a room. What is the probability that there is at least one shared birthday among these three people?
Solution:
There are a lot of ways there could be at least one shared birthday. Fortunately there is an easier way. We ask ourselves “What is the alternative to having at least one shared birthday?” In this case, the alternative is that there are no shared birthdays. In other words, the alternative to “at least one” is having none. In other words, since this is a complementary event,
P(at least one) = 1 – P(none)
We will start, then, by computing the probability that there is no shared birthday. Let’s imagine that you are one of these three people. Your birthday can be anything without conflict, so there are 365 choices out of 365 for your birthday. What is the probability that the second person does not share your birthday? There are 365 days in the year (let’s ignore leap years) and removing your birthday from contention, there are 364 choices that will guarantee that you do not share a birthday with this person, so the probability that the second person does not share your birthday is 364/365. Now we move to the third person. What is the probability that this third person does not have the same birthday as either you or the second person? There are 363 days that will not duplicate your birthday or the second person’s, so the probability that the third person does not share a birthday with the first two is 363/365.
We want the second person not to share a birthday with you and the third person not to share a birthday with the first two people, so we use the multiplication rule:
[latex]P(\text{nosharedbirthday})=\frac{365}{365}\cdot\frac{364}{365}\cdot\frac{363}{365}\approx0.9918[/latex]
and then subtract from 1 to get
P(shared birthday) = 1 – P(no shared birthday) = 1 – 0.9918 = 0.0082.
This is a pretty small number, so maybe it makes sense that the answer to our original problem will be small. Let’s make our group a bit bigger.
Suppose five people are in a room. What is the probability that there is at least one shared birthday among these five people?
Solution:
Continuing the pattern of the previous example, the answer should be
[latex]P(\text{sharedbirthday})=1-\frac{365}{365}\cdot\frac{364}{365}\cdot\frac{363}{365}\cdot\frac{362}{365}\cdot\frac{361}{365}\approx0.0271[/latex]
Note that we could rewrite this more compactly as
[latex]P(\text{sharedbirthday})=1-\frac{{}_{365}{{P}_{5}}}{{{365}^{5}}}\approx0.0271[/latex]
which makes it a bit easier to type into a calculator or computer, and which suggests a nice formula as we continue to expand the population of our group.
Suppose 30 people are in a room. What is the probability that there is at least one shared birthday among these 30 people?
Solution:
Here we can calculate
[latex]P(\text{sharedbirthday})=1-\frac{{}_{365}{{P}_{30}}}{{{365}^{30}}}\approx0.706[/latex]
which gives us the surprising result that when you are in a room with 30 people there is a 70% chance that there will be at least one shared birthday!
The birthday problem is examined in detail in the following.
If you like to bet, and if you can convince 30 people to reveal their birthdays, you might be able to win some money by betting a friend that there will be at least two people with the same birthday in the room anytime you are in a room of 30 or more people. (Of course, you would need to make sure your friend hasn’t studied probability!) You wouldn’t be guaranteed to win, but you should win more than half the time.
This is one of many results in probability theory that is counterintuitive; that is, it goes against our gut instincts.
Try It
Suppose 10 people are in a room. What is the probability that there is at least one shared birthday among these 10 people?
Expected Value
Repeating Procedures Over Time
Expected value is perhaps the most useful probability concept we will discuss. It has many applications, from insurance policies to making financial decisions, and it’s one thing that the casinos and government agencies that run gambling operations and lotteries hope most people never learn about.
example
In the casino game roulette, a wheel with 38 spaces (18 red, 18 black, and 2 green) is spun. In one possible bet, the player bets $1 on a single number. If that number is spun on the wheel, then they receive $36 (their original $1 + $35). Otherwise, they lose their $1. On average, how much money should a player expect to win or lose if they play this game repeatedly?
Solution:
Suppose you bet $1 on each of the 38 spaces on the wheel, for a total of $38 bet. When the winning number is spun, you are paid $36 on that number. While you won on that one number, overall you’ve lost $2. On a per-space basis, you have “won” -$2/$38 ≈ -$0.053. In other words, on average you lose 5.3 cents per space you bet on.
We call this average gain or loss the expected value of playing roulette. Notice that no one ever loses exactly 5.3 cents: most people (in fact, about 37 out of every 38) lose $1 and a very few people (about 1 person out of every 38) gain $35 (the $36 they win minus the $1 they spent to play the game).
There is another way to compute expected value without imagining what would happen if we play every possible space. There are 38 possible outcomes when the wheel spins, so the probability of winning is [latex]\frac{1}{38}[/latex]. The complement, the probability of losing, is [latex]\frac{37}{38}[/latex].
Summarizing these along with the values, we get this table:
| Outcome | Probability of outcome |
| $35 | [latex]\frac{1}{38}[/latex] |
| -$1 | [latex]\frac{37}{38}[/latex] |
Notice that if we multiply each outcome by its corresponding probability we get [latex]\$35\cdot \frac{1}{38}=0.9211[/latex] and [latex]-\$1\cdot \frac{37}{38}=-0.9737[/latex], and if we add these numbers we get
0.9211 + (-0.9737) ≈ -0.053, which is the expected value we computed above.
Expected Value
- Expected Value is the average gain or loss of an event if the procedure is repeated many times.
We can compute the expected value by multiplying each outcome by the probability of that outcome, then adding up the products.
Try It
You purchase a raffle ticket to help out a charity. The raffle ticket costs $5. The charity is selling 2000 tickets. One of them will be drawn and the person holding the ticket will be given a prize worth $4000. Compute the expected value for this raffle.
Example
In a certain state’s lottery, 48 balls numbered 1 through 48 are placed in a machine and six of them are drawn at random. If the six numbers drawn match the numbers that a player had chosen, the player wins $1,000,000. If they match 5 numbers, then win $1,000. It costs $1 to buy a ticket. Find the expected value.
Solution:
Earlier, we calculated the probability of matching all 6 numbers and the probability of matching 5 numbers:
[latex]\frac{{}_{6}{{C}_{6}}}{{}_{48}{{C}_{6}}}=\frac{1}{12271512}\approx0.0000000815[/latex] for all 6 numbers,
[latex]\frac{\left({}_{6}{{C}_{5}}\right)\left({}_{42}{{C}_{1}}\right)}{{}_{48}{{C}_{6}}}=\frac{252}{12271512}\approx0.0000205[/latex] for 5 numbers.
Our probabilities and outcome values are:
| Outcome | Probability of outcome |
| $999,999 | [latex]\frac{1}{12271512}[/latex] |
| $999 | [latex]\frac{252}{12271512}[/latex] |
| -$1 | [latex]1-\frac{253}{12271512}=\frac{12271259}{12271512}[/latex] |
The expected value, then is:
[latex]\left(\$999,999 \right)\cdot \frac{1}{12271512}+\left( \$999\right)\cdot\frac{252}{12271512}+\left(-\$1\right)\cdot\frac{12271259}{12271512}\approx-\$0.898[/latex]
On average, one can expect to lose about 90 cents on a lottery ticket. Of course, most players will lose $1.
View more about the expected value examples in the following video.
In general, if the expected value of a game is negative, it is not a good idea to play the game, since on average you will lose money. It would be better to play a game with a positive expected value (good luck trying to find one!), although keep in mind that even if the average winnings are positive it could be the case that most people lose money and one very fortunate individual wins a great deal of money. If the expected value of a game is 0, we call it a fair game, since neither side has an advantage.
Try It
A friend offers to play a game, in which you roll 3 standard 6-sided dice. If all the dice roll different values, you give him $1. If any two dice match values, you get $2. What is the expected value of this game? Would you play?
Expected value also has applications outside of gambling. Expected value is very common in making insurance decisions.
Example
A 40-year-old man in the U.S. has a 0.242% risk of dying during the next year.[1] An insurance company charges $275 for a life-insurance policy that pays a $100,000 death benefit. What is the expected value for the person buying the insurance?
Solution:
The probabilities and outcomes are
| Outcome | Probability of outcome |
| $100,000 – $275 = $99,725 | 0.00242 |
| -$275 | 1 – 0.00242 = 0.99758 |
The expected value is ($99,725)(0.00242) + (-$275)(0.99758) = -$33.
The insurance applications of expected value are detailed in the following video.
Not surprisingly, the expected value is negative; the insurance company can only afford to offer policies if they, on average, make money on each policy. They can afford to pay out the occasional benefit because they offer enough policies that those benefit payouts are balanced by the rest of the insured people.
For people buying the insurance, there is a negative expected value, but there is a security that comes from insurance that is worth that cost.
Attributions
This chapter contains material taken from Math in Society (on OpenTextBookStore) by David Lippman, and is used under a CC Attribution-Share Alike 3.0 United States (CC BY-SA 3.0 US) license.
This chapter contains material taken from of Math for the Liberal Arts (on Lumen Learning) by Lumen Learning, and is used under a CC BY: Attribution license.
- According to the estimator at http://www.numericalexample.com/index.php?view=article&id=91 ↵